Asymptotic expansion for a linear first-order ordinary difference equation (OΔE) with an irregular singular point at infinity:
In[475]:=
s=AsymptoticRSolveValue[y[n+1]3ny[n],y[n],{n,∞,4}]
Out[475]=
n
3

1-
571
2488320
4
n
-
139
51840
3
n
+
1
288
2
n
+
1
12n
-
1
2
+n
n

1
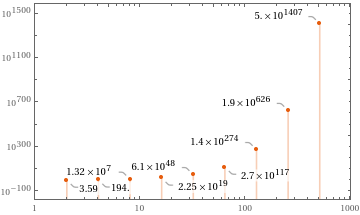
Plot the solution using a logarithmic scale:
In[478]:=
DiscretePlotCallouts/.{

1
1},
TraditionalForm[
]
,{n,2^Range[1,9]},ScalingFunctions{"Log","Log"},

Out[478]=
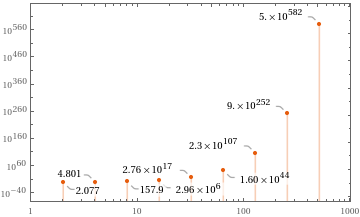
Plot the solution of an asymptotic expansion for a linear third-order OΔE with an irregular singular point:
In[479]:=
s=AsymptoticRSolveValue[y[n+3]-y[n]-(n+2)y[n+1]0,y[n],{n,∞,1}]
Out[479]=
n
(-)
1-
13
12n
-
3
2
-n
n

1
+
-n/2

1+
5
12n
-
1
n
n/2
n

2
+
n
(-1)
-n/2

1+
5
12n
+
1
n
n/2
n

3
In[483]:=
DiscretePlotCalloutN[s/.{

1
1,

2
1,

3
1},5],
TraditionalForm[
]
,{n,2^Range[9]},ScalingFunctions{"Log","Log"},

Out[483]=